Rattail — "Your Last Custom System"

Rattail is a collection of free software, designed for use in retail environments but useful in many others. It is available under the GNU General Public License, version 3.
Rattail is more of a framework and is not an "out of the box" system per se. However it provides many building blocks so that custom systems may be developed quickly using established patterns.
Its greatest strength is perhaps the integration capabilities, making it possible for various systems "in the wild" to talk to each other; each continuing to provide their unique features to your "overall" system, but with better (e.g. more accurate, customized) and more automated communication between them.
Concept
Here is a conceptual diagram of a "complete" Rattail system. The name "Poser" refers to a custom app built atop Rattail and Tailbone (the web app for Rattail). All systems on the right hand side of the graphic are external to Poser/Rattail, i.e. they are not "plugins" although Poser may use plugin-like logic for the sake of integrating with these systems.
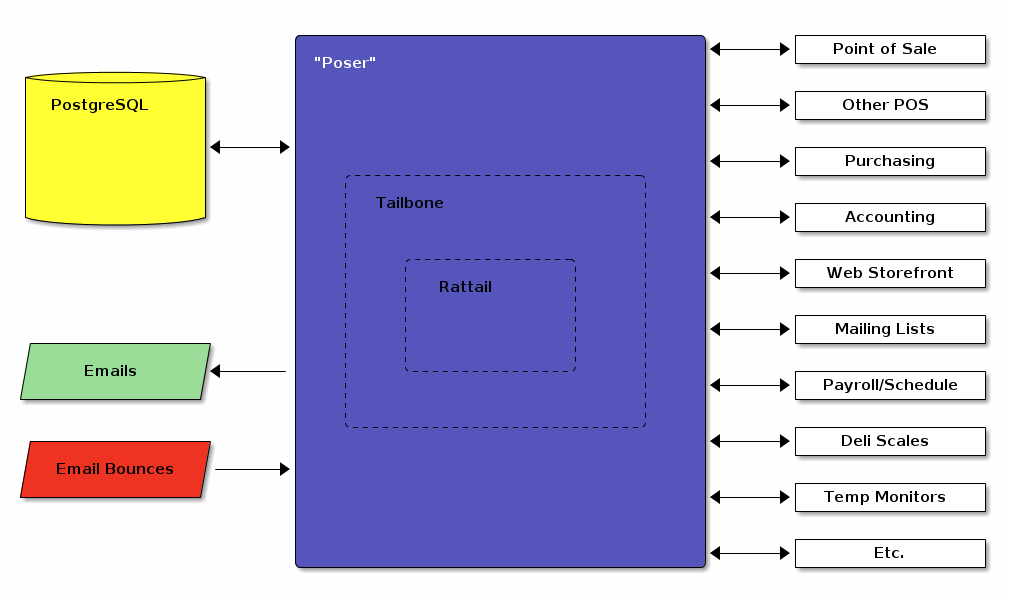
For more silly graphics, see here.
Integration / Solution Scenarios
Below is the "complete" (sic) list of problem patterns which Rattail aims to solve.
A good rule of thumb is, Rattail can usually replace "spreadsheet intervention" (manual manipulation and massaging of data) which is so often the "alternative" to a Rattail solution.
Note that how well Rattail can solve any particular problem, may vary depending on the nature of the other system(s) involved and overall complexity etc.
System A cannot talk to System B
And often, vice versa. This is a common scenario to say the least. Each system may expose e.g. some sort of API for integration, but there is no existing "plugin" etc. which can bridge the gap between the two systems.
Systems A and B "can talk" but do so "poorly"
Sometimes two systems "support" talking to each other (e.g. via some plugin), but in practice it just doesn't work for your needs. Maybe you want to avoid creating new records in the target system in only certain cases, or you need to "morph" some field values along the way, etc. Perhaps you need to add "real-time" sync somehow.
Systems can talk but do not track sufficient data
For instance, maybe you have good POS (point of sale) and CRM (customer relations management) systems in place and communicating just fine, but there is some small data piece missing, e.g. you have no way to track each customer's "favorite color" (or whatever). More likely, you may need to track certain extra customer-related attributes for each POS transaction, e.g. customer's membership status when it occurred.
Systems can talk but the user interface(s) is "poor"
For instance, your POS system has a "receiving" UI but it's clunky, and (if it supports it) a parallel UI may be used to facilitate better workflow for the humans involved. Another example is importing new product or customer records, often a custom UI can make that far more efficient.
No way to see and/or report on data from "all systems" in one place
Finally there is the "big" picture, something to tie it all together... For instance you have basic transaction reports from your POS, but your CRM has more detailed customer info and you'd like a report to combine that data somehow. Or maybe you just want to be able to see a given customer's favorite color and last transaction date/time on the same webpage.
One or more systems are "missing" from the picture
At some point the question arises, do I even need system X? Can my Rattail system just do "that thing(s)" instead? In some cases the answer may very well be yes, although it certainly depends on the thing(s) as that is not a primary goal for Rattail. For sake of example, if all you need from a CRM is a "container" for customer data plus certain special logic for it, Rattail could probably be your CRM. Note however that its UI is simplistic, unless you take steps to enhance it.
Typical Life Cycle of a Rattail System
YMMV of course, but this outcome is just as (and probably more) likely as any other!
- birth, to solve "one" problem
-
enhanced, to solve "one more" problem
- (this step is repeated, as needed)
- (there is no death!)
Getting Started
Please see the Quick Start guide.